ベイズ推定のキホン

■ 概要

• ベイズ推定を理解するために、「ベイズの定理」からの論理展開・考え方をまとめる。
  （このページでは、MCMCを使った推定、モデリング等には言及しない）
• 理解の助けに、例題と Python の基本ライブラリを使ったコードスニペットを示す。

■「ベイズの定理」の導出

「ベイズの定理」は「条件付確率」から次のように導出する。

条件付確率（ある事象Aが起こったという条件の下で別の事象Bが起こる確率）: \[ P(B|A) = \frac{P(A \cap B)}{P(A)} \tag{1} \]

両辺にP(A)を掛けて左辺と右辺を入れ替えると、以下が得られる。

乗法定理: \[ P(A \cap B) = P(B|A)P(A) \tag{2} \]

ここで右辺について、Aの役割をBに担わせれば（単なる記号でどっちでもいいので） \[ P(A \cap B) = P(A|B)P(B) \tag{3} \] に変換でき、当然 (2) の右辺と等値なので、 \[ P(A|B)P(B) = P(B|A)P(A) \tag{4} \] が得られる。これを \( P(A|B) \) について解くと、以下が得られる。

ベイズの定理（基本版）: \[ P(A|B) = \frac{P(B|A)P(A)}{P(B)} \tag{5} \]

事象Bが起こったときに事象Aが起きる確率を、事象Aが起こった時に事象Bが起こる確率で表現する、すなわち「逆確率」の関係を提示す。 ベイズ統計では、ある事象Aが起こる確率P(A)のことを 事前確率、その条件の下で別の事象Bが起こる確率 P(A|B) のことを 事後確率 と呼ぶ。

式を変換しただけで、「ベイズの定理 は 条件付確率 そのものである」と理解するのがポイント

■ 「ベイズの定理」を実用的な式に変換

上記で得られたベイズの定理（基本版）を汎化させ、実用的な形に変形する。
まずは、これまで単体で扱っていた事象\( A \)を、事象\( A_1 \)、\( A_2 \)、\( A_3 \) という３つの排反事象に分割した場合を考える。

ある事象が複数に分割されたとき、それぞれの確率を足し上げると1（= 100%）、つまり以下のようになる点に留意。 \[ \sum_{i=1}^{a}P(A_i) = 1 \tag{6} \]

ベイズの定理（基本版）の \( A \) を \( A_1 \) に書き換えれば単に \[ P(A_1|B) = \frac{P(B|A_1)P(A_1)}{P(B)} \tag{7} \]

と書ける。ここで、事象Bの確率 \( P(B) \) は、事象 \( A_1 \)、\( A_2 \)、\( A_3 \) ３つとの同時確率の和で表現できる。 \[ P(B) = P(B \cap A_1) + P(B \cap A_2) + P(B \cap A_3) \tag{8} \]

上式の右辺を（2）により次のように変換する。 \[ P(B) = P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + P(B|A_3)P(A_3) \tag{9} \]

これを（7）に代入すると、 \[ P(A_1|B) = \frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + P(B|A_3)P(A_3)} \tag{10} \]

と書ける。これを一般化すると、

ベイズの定理（汎用版）: \[ P(A_i|B) = \frac{P(B|A_i)P(A_i)}{\sum_{i=1}^{a}P(B|A_i)P(A_i)} \tag{11} \]

が得られる。

---

数学の文章問題では、「排反事象をいくつに分割するか」を考えることが解答のポイントになったりする。

例題
赤玉と白玉が入った袋が2つ存在する。（それぞれA、Bとする） 袋Aには赤玉🔴が2つ、白玉⚪️が1つはいっている。袋Bには赤玉🔴が1つ、白玉⚪️が4つはいっている。 ある人がどちらかの袋から玉をひとつ取り出し、あなたにその玉の色だけを伝える。そのとき選ばれた袋がAである確率を推定せよ。

解答
・袋Aから赤玉を取り出す確率: \( P(🔴|A) = 2/3 \) ← 問題文より
・袋Aから白玉を取り出す確率: \( P(⚪️|A) = 1/3 \) ← 問題文より （※\( 1 - P(🔴|A) \)）
・袋Bから赤玉を取り出す確率: \( P(🔴|B) = 1/5 \) ← 問題文より
・袋Bから白玉を取り出す確率: \( P(⚪️|B) = 4/5 \) ← 問題文より （※\( 1 - P(🔴|B) \)）
・袋Aから赤玉を取り出す確率: \( P(A) = 1/2 \) ← 理由不十分の原則より
・袋Bから赤玉を取り出す確率: \( P(B) = 1/2 \) ← 理由不十分の原則より

取り出した玉が赤玉だった場合、選ばれた袋がAである確率は

\begin{align} P(A|🔴) &= \cfrac{P(🔴|A)P(A)}{P(🔴|A)P(A) + P(🔴|B)P(B)} \\ &= \cfrac{2/3 \times 1/2}{(2/3 \times 1/2) + (1/5 \times 1/2)} \\ &= \cfrac{10}{13} \approx 76.92 \% \end{align}

取り出した玉が白玉だった場合、選ばれた袋がAである確率は

\begin{align} P(A|⚪️) &= \cfrac{P(⚪️|A)P(A)}{P(⚪️|A)P(A) + P(⚪️|B)P(B)} \\ &= \cfrac{1/3 \times 1/2}{(1/3 \times 1/2) + (4/5 \times 1/2)} \\ &= \cfrac{5}{17} \approx 29.41 \% \end{align}

---

■ ベイズ推定の方法

ベイズの定理を「確率」から「分布」に拡張して説明する。

◇ ベイズ統計における「原因」と「結果」

通常の条件付確率では、因果関係は時系列順に P(結果｜原因) というように、「原因から結果」の確率を求めるが、ベイズの定理では、時間の流れに逆らって「結果から原因」の確率 P(原因｜結果) を求めようとする。

◇ 原因（仮定 \( H \) ）と結果（観測データ \( D \) ）を考える

事象Aを「原因（仮定: Hypothesis）」、事象Bを「その結果の事象（観測データ: Data）」と読み替えると、ベイズの定理は次のように書き換えて解釈できる。 \[ P(H|D) = \cfrac{P(D|H)P(H)}{P(D)} \tag{12} \] \[ P(H_i|D) = \frac{P(D|H_i)P(H_i)}{\sum_{i=1}^{a}P(D|H_i)P(H_i)} \tag{13} \]

このように変換することで、「観測データDという結果が与えられたとき、その原因が、特定の仮定Hである確率」を求める式として利用できる。

◇ 原因（仮定 \( H \) ）を確率分布のパラメーター \( \theta \) に置き換える

統計モデルでは、確率分布の性質によって現象の説明や予測ができるようになるため、確率分布のパラメーター推定は重要なテーマ。「ベイズの定理」を役立てるには、仮定 \( H \) を「パラメーターが \( \theta \) をとるときの確率分布」と読み替える必要がある。これをベイズの定理について言い換えると、次のようになる。 \[ P(\theta|D) = \cfrac{P(D|\theta)P(\theta)}{P(D)} \tag{14} \] \[ P(\theta_i|D) = \frac{P(D|\theta_i)P(\theta_i)}{\sum_{i=1}^{a}P(D|\theta_i)P(\theta_i)} \tag{15} \]

◇ パラメーター \( \theta \) は連続変数として捉え直す

一般に、確率分布のパラメーターは連続変数である。「ベイズの定理」では計算を「事前確率」や「事後確率」というようにスポットでの確率計算が課題意識だったが、これを連続数に対応して「事前分布」「事後分布」という形で捉え直す。

・事前確率 \( P(\theta) \) → 事前分布 \( \pi (\theta) \)
・尤度 \( P(D|\theta) \) → 尤度 \( f(\theta) \)
・事後確率 \( P(\theta|D) \) → 事後分布 \( \pi (\theta|D) \)

ベイズの定理（分布対応版）:
\[ \pi(\theta|D) = \cfrac{f(D|\theta)\pi(\theta)}{P(D)} \tag{16} \]

◇ 正規化定数 \( k \) とカーネル

(16) の右辺分母としている \( P(D) \) は、「観測データ \( D \) が得られる確率」を意味するが、実際に分析する場面では、多くの場合データは所与であるため重要ではない。より論点をクリアにするために正規化定数 \( k \) をつかって \[ \pi(\theta|D) = kf(D|\theta)\pi(\theta) \tag{17} \] と表すことがある。また、確率分布のパラメーター \( \theta \) を含んでいる右辺の \( f(D|\theta)\pi(\theta) \) のことを カーネル と呼び、その確率分布の本質的な性質を決定づけている。
実務においては、調整役の正規化定数 \( k \) をいちいち式に明示することなく、単に比例定数としてカーネルを強調するような書き方をする場合が多い。

ベイズの定理（簡易版）:
\[ 事後分布 \propto 尤度 \times 事前分布 \] \[ \pi(\theta|D) \propto f(D|\theta)\pi(\theta) \tag{18} \]

---

「ベイズ推定」の利用イメージを膨らませるために、シンプルな例題を Python で解く。

例題
表が出る確率が \( \theta \) である1枚のコインがある。 このコインを5回投げた時、{表、表、裏、表、裏}の順に出た。 このとき、表の出る確率 \( \theta \) の事後分布 \( \pi (\theta | D) \) を求めよ。

解答
まずは \( \pi(\theta|D) \propto f(D|\theta)\pi(\theta) \) を思い出す。

・コインの表が出る確率: \( f(表| \theta) = \theta \)
・コインの裏が出る確率: \( f(裏| \theta) = 1 - \theta \)
・事前分布: \( \pi(\theta) = 1 \space (0 \leq \theta \leq 1) \)
　┗ 「理由不十分の原則」より、事前分布 \(\pi (\theta) \)を「一様分布」とする。

観測データが5回分ある状況において、事後分布が変化する過程を matplotlib で示す。

import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
# 事前分布として一様分布を設定
def pi_0(theta):
    return 1.0

def veiw_pi(pi):
    '''事後分布の形を描画'''
    fig = plt.figure(figsize = (10, 5))
    ax = plt.axes()
    
    theta = np.arange(0,1.1,.1)
    ax.plot(theta, [pi(t) for t in theta])
    ax.set_ylabel(' $\pi(\\theta)$ ')
    ax.set_xlabel(' $\\theta$ ')
    ax.grid(True);

veiw_pi(pi_0)

[Out:]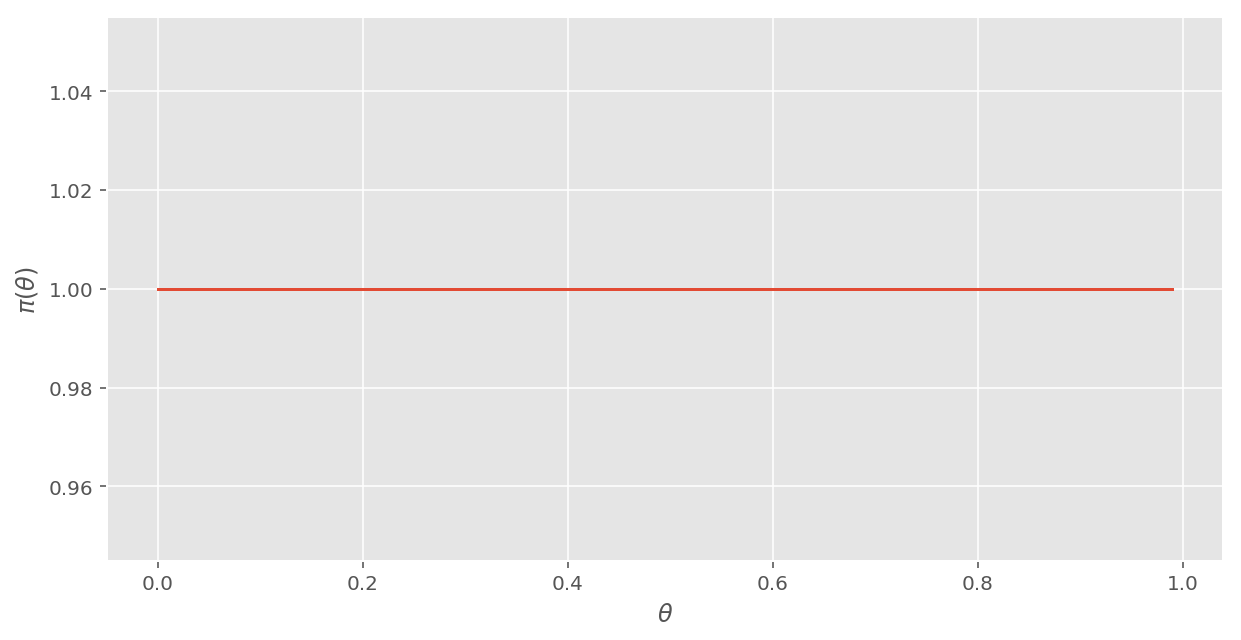

この事前分布に対して、「1回目に表が出た」という観測データを取り込む。 「1回目に表が出る」という事象を \( D_1 \) とすると、尤度は \( f(表|\theta) = \theta \) で示されるため、

1回目の事後分布（表）: \( \pi(\theta|D_1) \propto \color{red} \theta \color{black} \times 1 = \color{red} \theta \)

※反映箇所を赤く示しています。

\( (0 \leq \theta \leq 1) \) の定義域で確率の総和が1という条件から、正規化定数は \( k = 2 \) と求まる。1回目のデータを取り込んだという意味で、\( \pi_1(\theta) \) と表記すれば、 \[ \pi_1(\theta) = 2\theta \] となり、グラフで示すと次のようになる。

# ベイズ更新 1
def pi_1(theta):
    return 2 * theta
    
veiw_pi(pi_1)

[Out:]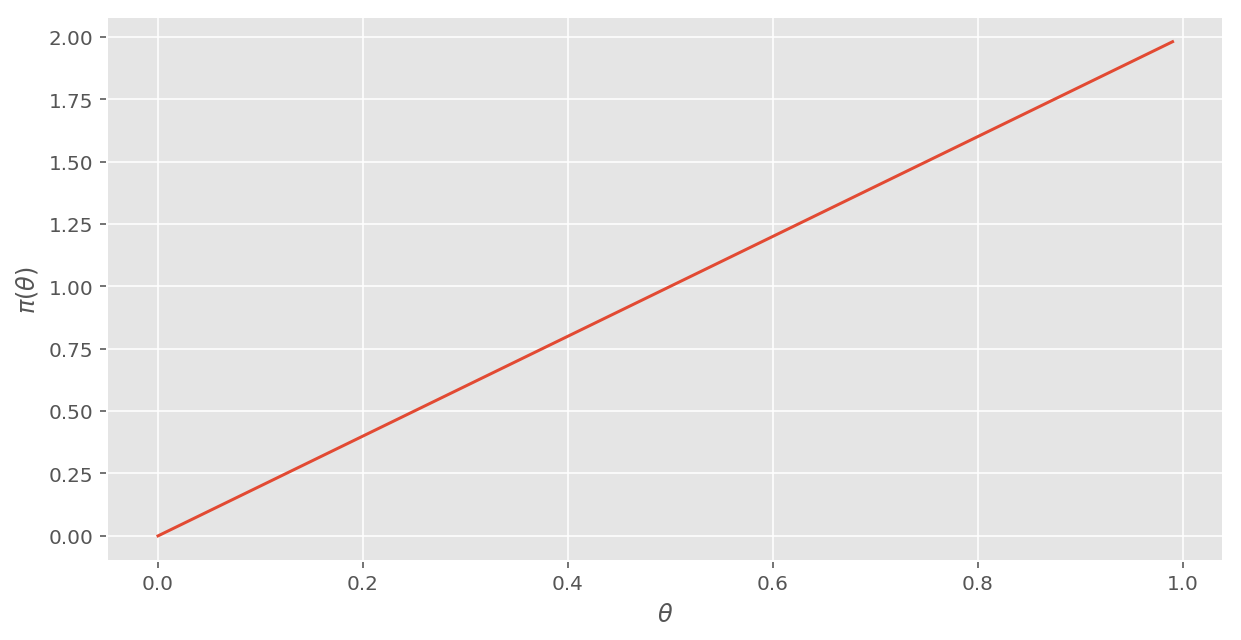

さらに、「2回目に表が出た」という事象を \( D_2 \) とすると、1回目と同様に、尤度は \( f(表|\theta) = \theta \) で示されるため、2回目の事後分布を1回目の事前分布に掛け合わせて、

2回目の事後分布（表）: \( \pi(\theta|D_2) \propto \color{red} \theta \color{black} \times 2 \theta = 2 \color{red} \theta^2 \)

\( (0 \leq \theta \leq 1) \) の定義域で確率の総和が1という条件から、正規化定数は \( k = 3 \) と求められ、 \[ \pi_2(\theta) = 3\theta ^2 \] となり、グラフで示すと次のようになる。

# ベイズ更新 2
def pi_2(theta):
    return 3 * theta ** 2

veiw_pi(pi_2)

[Out:]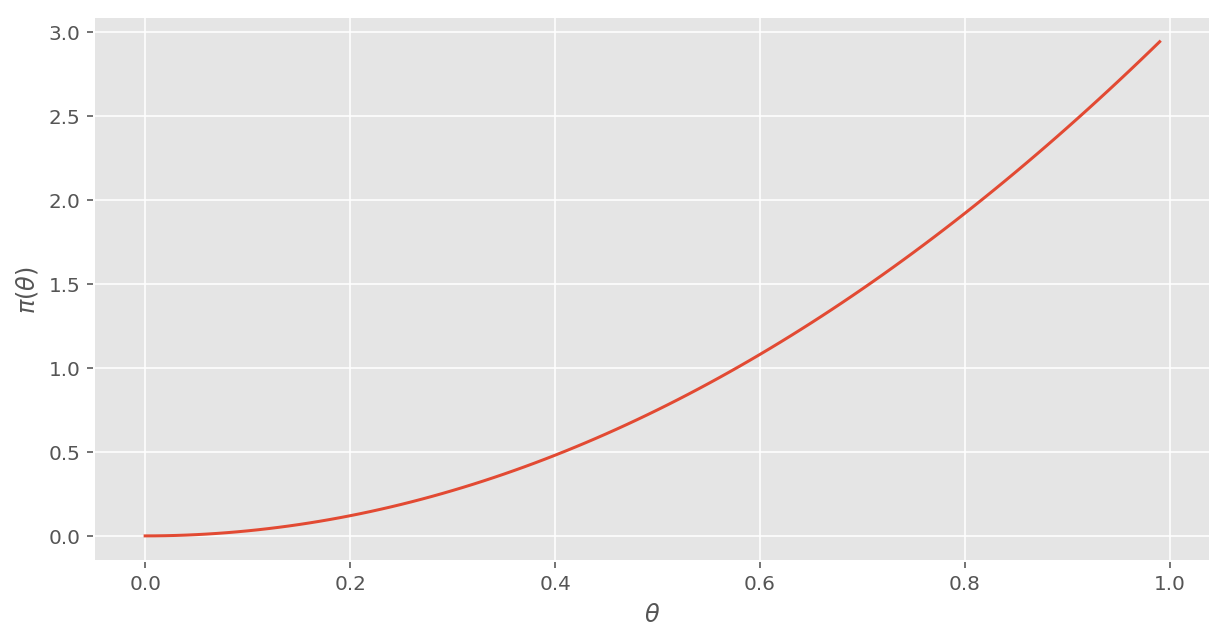

このように、事後分布となった結果を事前分布において、新たなデータを取り込んで次の事後分布を計算することを ベイズ更新 と呼ぶ。さらに「3回目：裏」「4回目：表」「5回目：裏」というデータを取り込んでベイズ更新を進めると、これまでと同様に、

3回目の事後分布（裏）: \( \pi(\theta|D_3) \propto \color{red}(1 - \theta) \color{black} \times 3\theta^2 = 3 \color{red} (1 - \theta) \color{black} \theta^2 \)

規格化の条件より、正規化定数は \( k = 12 \) なので、 \[ \pi_3(\theta|D_3) = 12(1-\theta)\theta^2 \]

4回目の事後分布（表）: \( \pi(\theta|D_4) \propto \color{red} \theta \color{black} \times 12(1-\theta)\theta^2 = 12(1-\theta)\color{red} \theta^3 \)

規格化の条件より、正規化定数は \( k = 20 \) なので、 \[ \pi_4(\theta|D_4) = 20(1-\theta)\theta^3 \]

5回目の事後分布（裏）: \( \pi(\theta|D_5) \propto \color{red} (1 - \theta) \color{black} \times 20(1-\theta)\theta^3 = 20 \color{red} (1-\theta)^2 \color{black} \theta^3 \)

規格化の条件より、正規化定数は \( k = 60 \) なので、この例題に対する回答は、以下となる。 \[ \underline{\pi_5(\theta|D_5) = 60(1-\theta)^2\theta^3} \]

尚、正規化定数 \( k \) は代数計算ライブラリの SymPy を使い、積分計算で次のように求めることができる。

import sympy as sym
theta = sym.Symbol('theta')

sym.integrate((1 - theta) * theta ** 2, (theta, 0, 1))

[Out:] 1/12

sym.integrate((1 - theta) * theta ** 3, (theta, 0, 1))

[Out:] 1/20

sym.integrate(((1 - theta) ** 2) * (theta ** 3), (theta, 0, 1))

[Out:] 1/60

また、それぞれのグラフは次の通り。

# ベイズ更新 3
def pi_3(theta):
    return 12 * (1 - theta) * theta ** 2

# ベイズ更新 4
def pi_4(theta):
    return 20 * (1 - theta) * theta ** 3

# ベイズ更新 5
def pi_5(theta):
    return 60 * ((1 - theta) ** 2) * (theta ** 3)

veiw_pi(pi_3)

[Out:]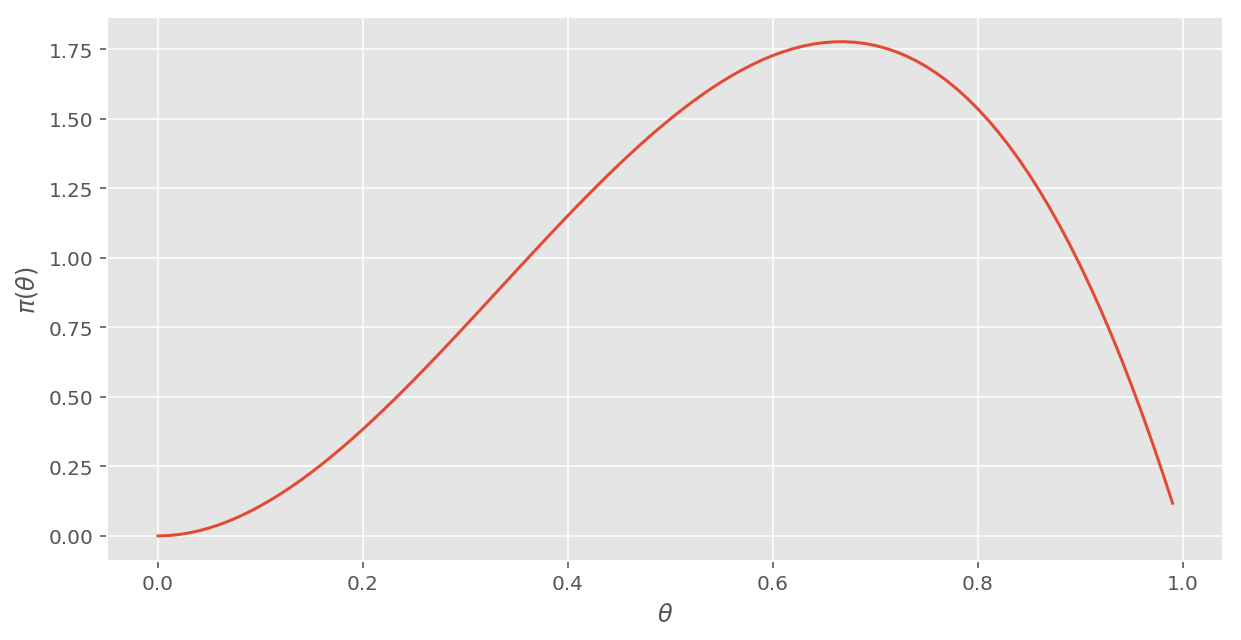

veiw_pi(pi_4)

[Out:]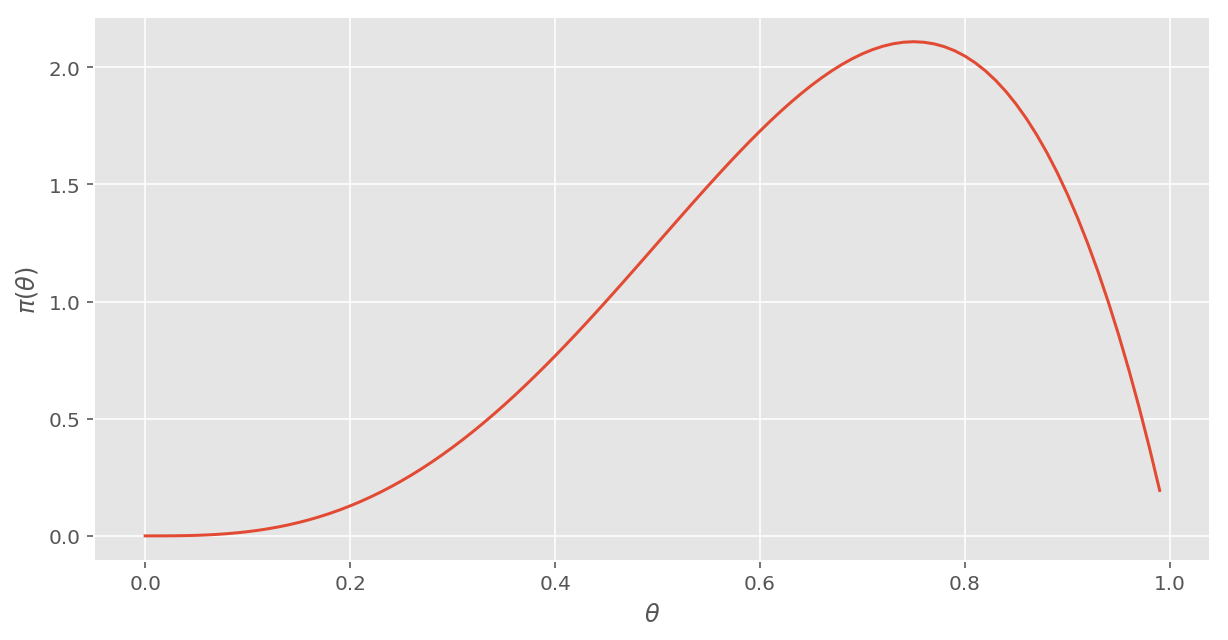

veiw_pi(pi_5)

[Out:]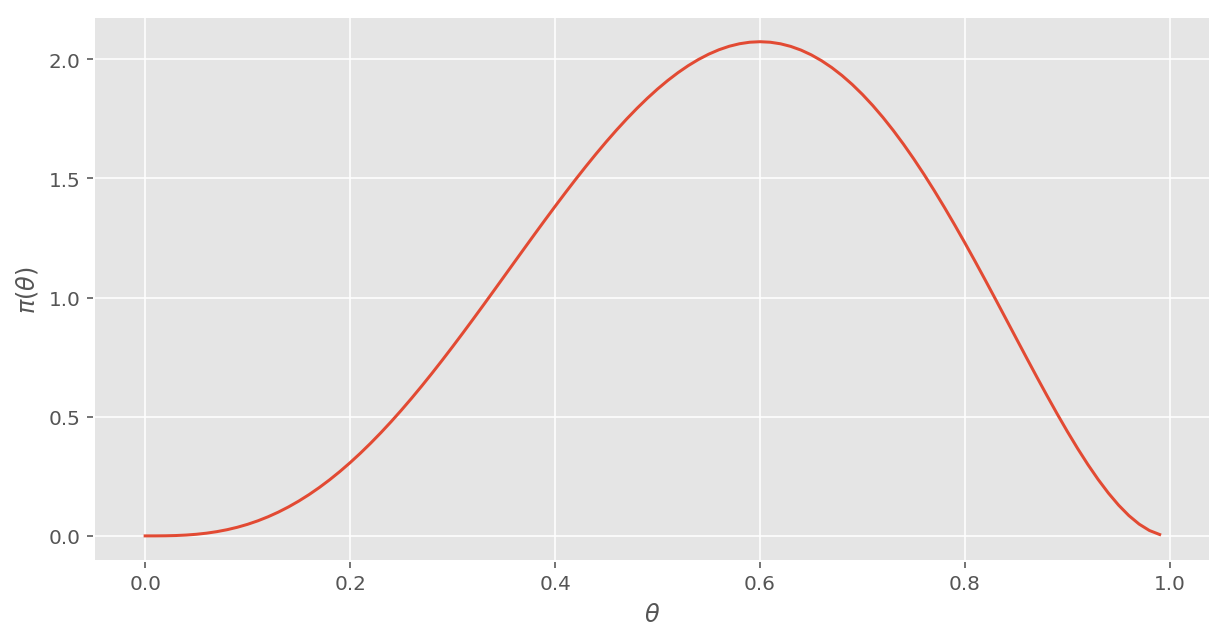

以上が、基本的なベイズ推定の考え方である。
ベイズ推定の際、MCMCで収束したら満足してしまう節があるが「これに至る理論背景ってどんなだっけ？」が曖昧だったため、整理した。

参考

• (2009) 涌井良幸, “道具としてのベイズ統計”
• (2015) 豊田秀樹, “基礎からのベイズ統計”