有意水準と検出力

適切なサンプルサイズを選ぶこと、\(\alpha\) エラー（第1種過誤）と \(\beta\) エラー（第2種過誤）を理解することが、効果的な A/B テスト実施の鍵。それらの理解に必要な 有意水準 と 検出力 とは何か、Python スクリプトと図解を交えて解説する。

■ 第1種の過誤（\(\alpha\)）と第2種の過誤（\(\beta\)）

まず、\(\alpha\) エラー（第1種過誤） とは、帰無仮説（\(H_0\)）が真であるにも関わらず、これを誤って棄却してしまうリスクを指す。
一方、\(\beta\) エラー（第2種過誤） は、対立仮説（\(H_1\)）が真の場合に、誤って帰無仮説を採択してしまうリスクである。
\(\alpha\) エラーを制御することは多くの研究で重視されるが、\(\beta\) エラーの制御も「真実を見逃すリスク」が高まるため軽視してはダメ。
\(\alpha\) は 有意水準 と呼ばれ、通常 0.05（5%）に設定されるが、\(\beta\) は 0.20（20%）が一般的で、これは検定の力 検出力（\(1-\beta\) ）が 80% であることを意味する。

■ サンプルサイズの選び方

サンプルサイズが小さすぎると、テストの感度（検出力）が低くなり、\(\beta\) エラーが高まる。
逆に、大きすぎるとテストのためのリソースを無駄に消費してしまうため、適切なサンプルサイズは、想定される「効果の大きさ（効果量）」、「\(\alpha\) エラー」、「\(\beta\) エラー」の設定に基づいて計算されるべきである。
詳しい計算例は、別ページ A/Bテストのためのサンプルサイズ計算にまとめているので参照。

■ Python による視覚的解説

Python スクリプトを用いて、これらの概念を視覚的に説明する。
以下のスクリプトは、「介入群（TG）」と「コントロール群（CG）」の平均の分布を描画し、\(\alpha\) エラーと \(\beta\) エラーを視覚化する。

# ライブラリ等
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
%config InlineBackend.figure_format = 'retina'

# 描画関数の定義
def plot_distributions(sample_size, tg_ratio, cg_mean, pooled_std, lift):
    
    # 各群のサンプルサイズ計算（cg: コントロール群、tg: 介入群）
    cg_n = int(sample_size / (1 + tg_ratio))
    tg_n = sample_size - cg_n

    # 各群の指標平均値をリフト幅から計算
    tg_mean = cg_mean * lift

    # 効果量の計算（Cohen's d）
    effect_size = (tg_mean - cg_mean) / pooled_std

    # 標準誤差（Standard Error）の計算
    cg_se = pooled_std / np.sqrt(cg_n)
    tg_se = pooled_std / np.sqrt(tg_n)

    # 帰無仮説、対立仮説それぞれの分布を計算
    x_range = np.linspace(cg_mean - 4 * cg_se, tg_mean + 4 * tg_se, 1000)
    y_cg = norm.pdf(x_range, cg_mean, cg_se)
    y_tg = norm.pdf(x_range, tg_mean, tg_se)

    # 有意水準を設定し、閾値と検出力を計算する
    alpha = 0.05
    critical_value = norm.ppf(1 - alpha, cg_mean, cg_se)
    power = 1 - norm.cdf(critical_value, tg_mean, tg_se)
    
    # 描画
    plt.figure(figsize = (10, 6))
    plt.plot(x_range, y_cg, label = 'Control Group ($H_0$: Null Hypothesis)', color = 'blue')
    plt.plot(x_range, y_tg, label = 'Treatment Group ($H_1$: Alternative Hypothesis)', color = 'red')
    plt.fill_between(x_range, 0, y_cg, where = (x_range > critical_value), color = 'blue', alpha = 0.3, label = 'Rejection Region (5% Significance)')
    plt.fill_between(x_range, 0, y_tg, where = (x_range > critical_value), color = 'red', alpha = 0.3, label = 'Power Region (Test Sensitivity)')
    plt.axvline(critical_value, color = 'grey', linestyle = '--', label = 'Critical Value')
    plt.title('Distribution of Means under $H_0$ and $H_1$')
    plt.xlabel('Mean')
    plt.ylabel('Density')
    plt.grid()
    plt.legend()
    plt.show()

    print("Mean CG: {:.2f}, Mean TG: {:.2f}".format(cg_mean, tg_mean))
    print("Effect Size (Cohen's d): {:.2f}".format(effect_size))
    print("Critical value: {:.2f}".format(critical_value))
    print("Power of the test: {:.2%}".format(power))

■ 実際に関数を呼び出して結果を確認する

関数の引数として、以下の条件を設定して A/B テストの結果を見てみる。

サンプルサイズ: 1,000
TG と CG のサンプルサイズ比率: 1:1
CG の指標平均値: 2.3
標準偏差（両群で同じ値を仮定）: 2
効果の大きさ（lift）: 110%（TG は CG の 110% 改善を仮定）

plot_distributions(sample_size = 1000, tg_ratio = 1, cg_mean = 2.3, pooled_std = 2, lift = 1.1)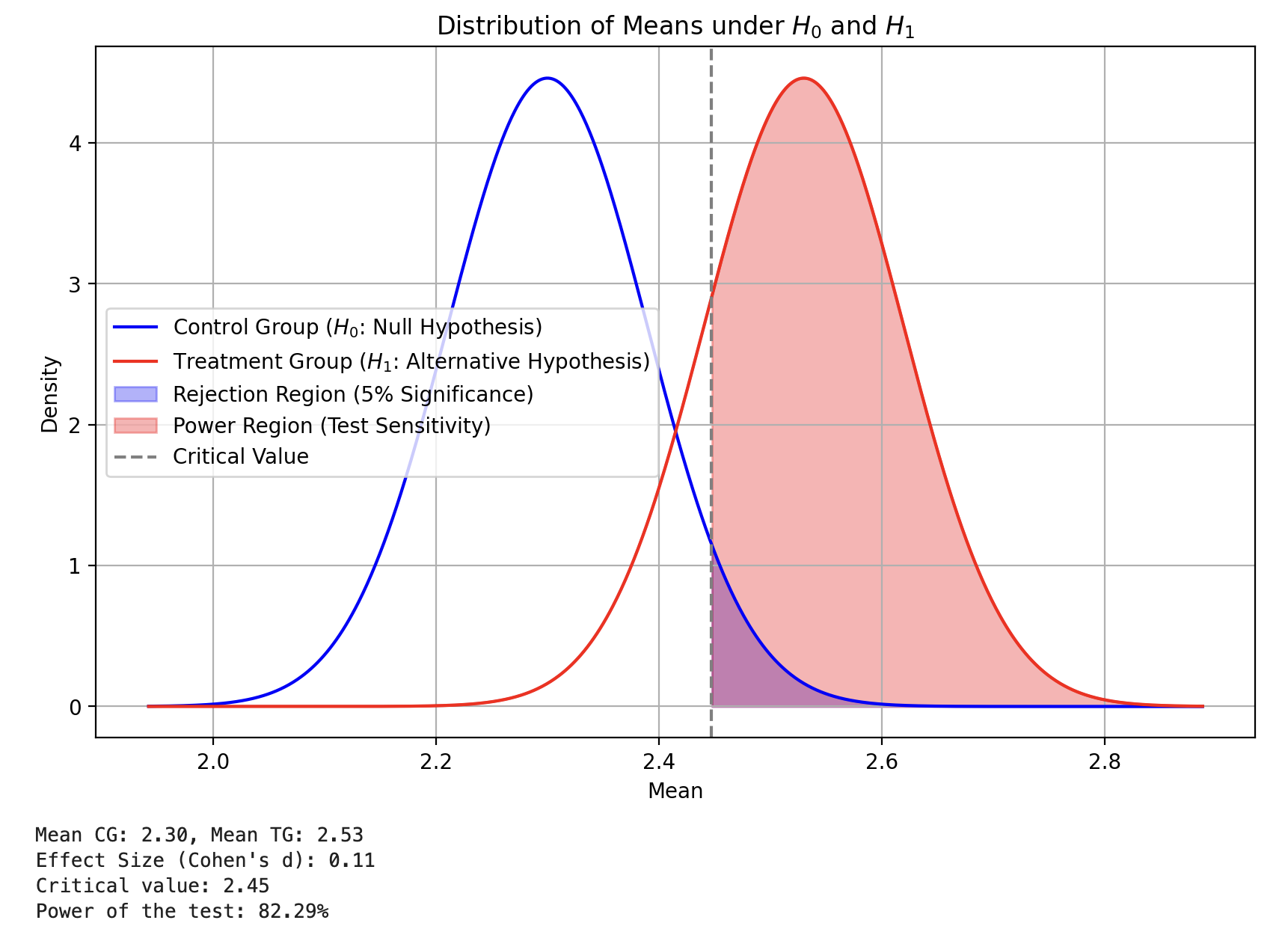

dist_base

CG と TG の平均値の分布を示し、特に 棄却領域（Rejection Region） と 検出力領域（Power Region） を色分けして表示している。点線の 閾値（Critical Value） を越える部分がどの程度存在するか、そして実際の効果がどれだけ検出可能かが視覚的にグラフで示されている。
閾値（Critical Value）は、\(\alpha\) エラーを制御するための値であり、この値以上の結果が得られた場合に帰無仮説を棄却する。検出力（テストの感度）は、実際に効果がある場合にその効果を正しく検出できる確率を示しており、サンプルサイズを増やすことでこの値を高めることができる。

■ サンプルサイズと効果の大きさの変更が結果に及ぼす影響

A/B テストでは、サンプルサイズ や 効果の大きさ（lift） を変えることによって、結果の解釈が大きく変わる可能性がある。ここでは、異なるシナリオを用いて、それぞれの変数が閾値と検出力にどのような影響を与えるかを確認しよう。

1. サンプルサイズの増加：

サンプルサイズを 3,000 に増やした結果の変化は以下：

plot_distributions(sample_size = 3000, tg_ratio = 1, cg_mean = 2.3, pooled_std = 2, lift = 1.1)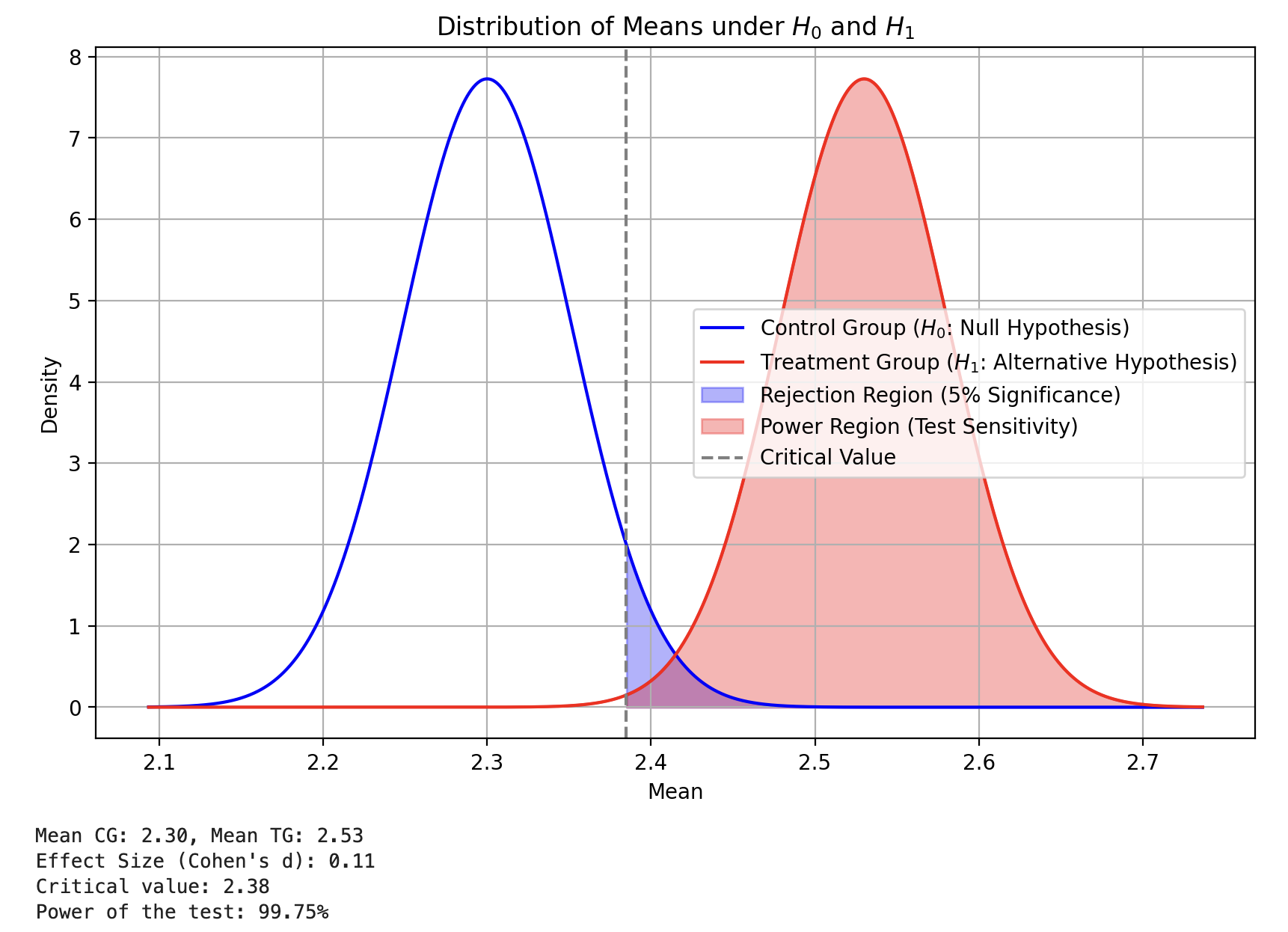

dist_sample3000

サンプルサイズを増やすと、標準誤差が減少し、分布がより狭く、ピークが高く なる。
これにより、平均値の違いがより明確に検出可能となり、検出力が向上 する。
統計的な「ノイズ」が減少するため、より小さい効果も検出 できるようになる。

2. 効果の大きさの増加：

効果の大きさを 1.3（30%の向上） に調整した場合の結果の変化は以下：

plot_distributions(sample_size = 1000, tg_ratio = 1, cg_mean = 2.3, pooled_std = 2, lift = 1.3)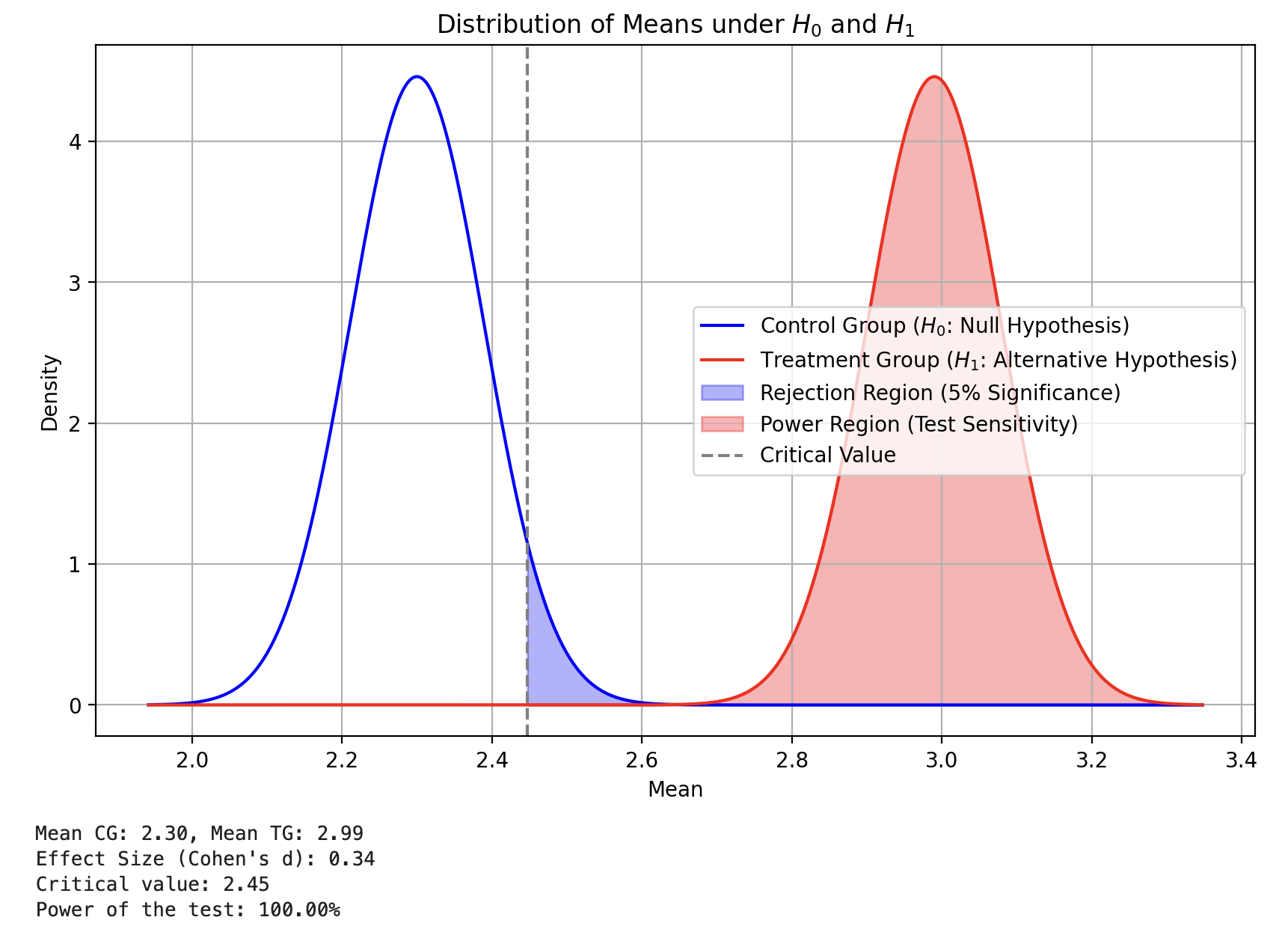

dist_effect130

効果の大きさが大きくなると、TG の平均値が CG の平均値から より離れる ことになる。
これにより、分布間の重なりが減少し、帰無仮説を棄却するための エビデンスが明確 になる。
結果として、検出力が向上 し、テストの有効性が高まる。

■ まとめ

A/B テストの計画において、テスト設計に対する正しい解釈とその根拠は、テストの信頼性の観点から非常に重要。きちんと準備しましょう。